Creating a Parliament Chart in Tableau

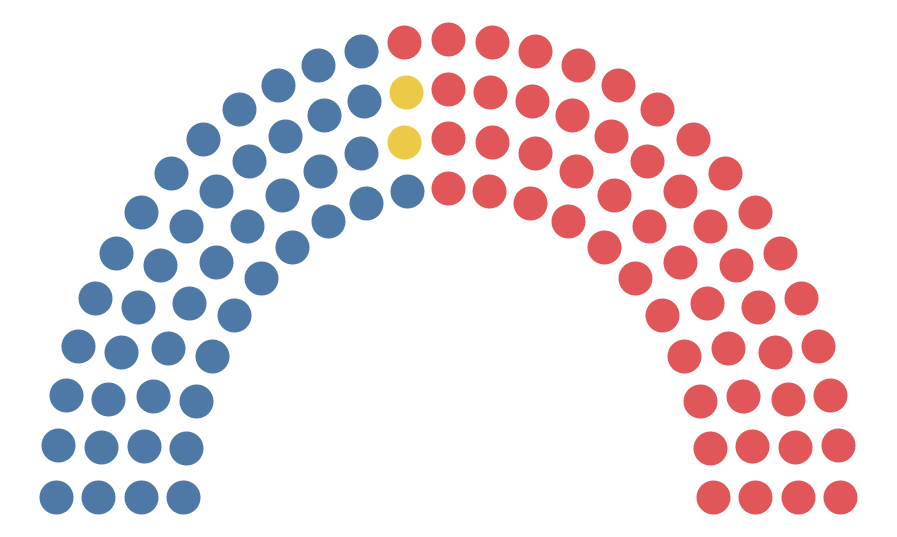
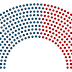
Parliament charts are a common method for showing the results of an election or the current makeup of a parliamentary government. These charts show each seat of the parliament in a semi-circle, similarly to the way seats might be arranged in a parliamentary chamber. For example, Wikipedia uses the following chart on their page for the 116^th Congress of the United States:

Wikipedia, By User: GoldRingChip - Parliament diagram tool, Public Domain

In January of 2019, I created a visualization analyzing the diversity of the 116th Congress and used a parliament chart show the difference between representational and actual gender diversity.

Before I even started this visualization, however, I had been working on some way to templatize these charts for use in Tableau. My primary goal was to make it completely flexibly so that you can show any number of seats and control the number of rows, the spacing between rows, the size of the dots, and the ordering/coloring. Unfortunately, this proved to be really difficult (for reasons I’ll get to shortly), so I never quite reached the finish line until now.

Iterations

As is normal for a complex chart like this, I went through a number of iterations to reach the final product. My first attempt was to use some fairly basic trigonometry to create the chart.

In this version, you can specify the number of rows, then it simply plots an equal number of seats on each arc. While this is okay, it had a couple of fundamental problems. First, it looks a bit strange when you don’t have enough seats to fill each row. For example, here’s the same chart with 12 rows instead of the 15 shown above:

A second issue is that, as you extend outward, the space between each dot gets greater. This is all space that could be filled and leaves the chart looking a bit sparse. So, I set out to come up with an option that would do the following:

1) Fill each entire row automatically.

2) Ensure equal spacing between each dot.

And here’s where it gets tricky. Because we’re drawing dots on multiple arcs that increase in radius, we’ll need to draw a different number of dots on each arc in order to maintain consistent spacing. Thus we need some math to determine how many dots to place on each arc, depending on a variety of different parameters being made available to the user (number of seats, number of rows, spacing, etc.).

To work through this, I started out by thinking how this would work if we were to draw each dot along a single horizontal line, kind of like this:

What would then happen if we were to break these up into multiple rows and wrap them around a semi-circle? To do this, we first need to know the number of arcs (or rows), so I created a parameter allowing the user to specify this number. We then need to know the length of each of those arcs. We can do that using the math to calculate the circumference: C=2πr. Since this is just half a circle, our formula becomes: C=πr. To get the radius, I created a parameter for the radius of the first row (set to 1, by default) and another to specify the spacing between each row. Using these, we can determine radius and, therefore, the length of each arc.

From here, we’ll get into some much more complex math, which I personally haven’t encountered since high-school. I’m not going to go into a ton of detail here due to the complexity, but I’ll do my best to explain it at a high level. In order to solve the number of dots which will go on each row, we can solve triangle numbers for a total of n different rows. In this case, however, the equation results in mixed n and n² numbers. This is called a quadratic equation and, to solve it, we need to use the quadratic formula.

Have I lost you? Sorry, this is tricky stuff and it took me a very long time to work through it myself. I’m not going to go into any further detail about the quadratic formula, but feel free to read through the link provided above if you’re interested in gaining a better understanding of how it works.

Having used the quadratic formula to solve my equation, I now knew how many dots to place on each row. Here is the same flat line colored by row (3 rows):

Notice that the number of dots increases for each row, exactly as we had planned.

In order to plot these on arcs, we’ll perform some trig. For that, we need the radius and the angle. We already have the radius for each row, so we need to determine an angle (from 0 to 180°) for each dot. We can do this by dividing 180 by the number of dots on the row. With that, we can complete the trig to plot them on their arcs.

When we connect to some real data (in this case, the 116^th US Senate), we get this:

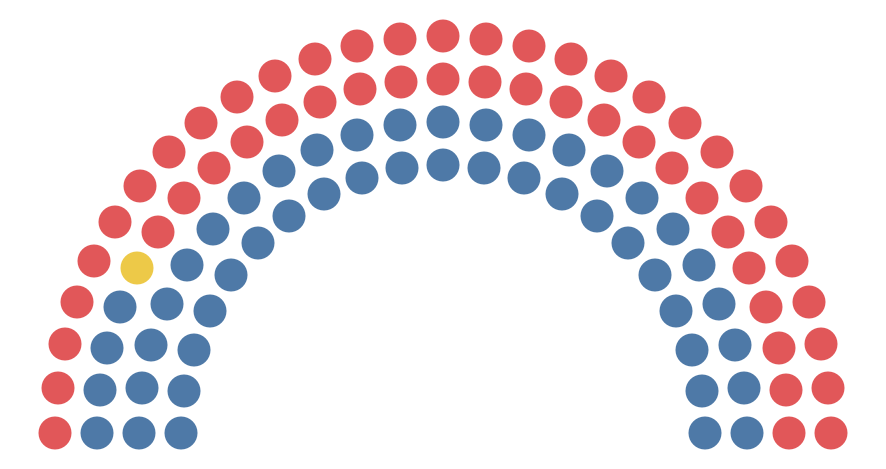
This has one fundamental flaw. Ideally, as in previous examples, each party would be confined to one area. We’d start with say the Democrats (blue) then fill in from the left, then add in the Independents (yellow), then fill in the rest with Republicans (red). But the above starts from the bottom up, rather than left to right.

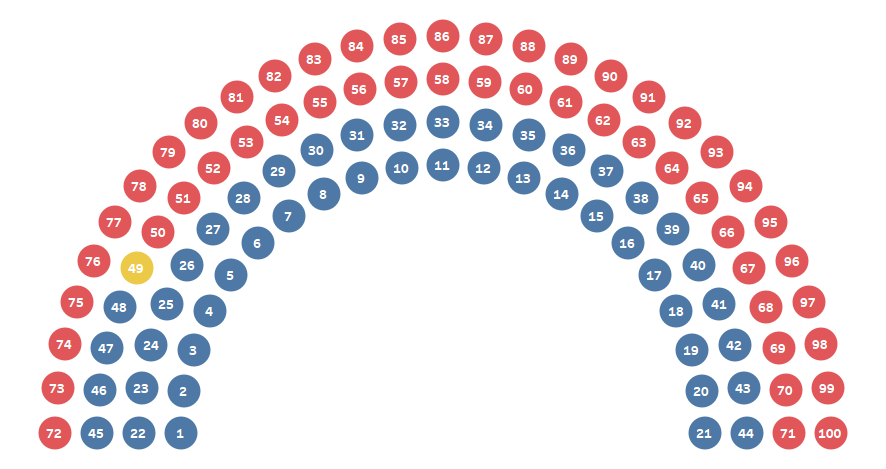
The problem is that this is how the arcs are drawn—starting with the first arc and drawing left-to-right, then moving to the next arc, etc. as shown below.

My data set was organized with a seat # and ordered the way I wanted to show them on the chart. So, in order to get them ordered properly, I’d need to either manually number each seat to force the grouping or find a new way to solve the math.

And that’s where I got stuck…

A Solution

This sat on the shelf for over a year, but after completing another project, I recently decided to take another look. Once again, I poured over the math, in an attempt to find away to reorder the numbers. I realized that I could use an INDEX table calculation, computed by the Angle in order to essentially renumber the dots in the desired manner.

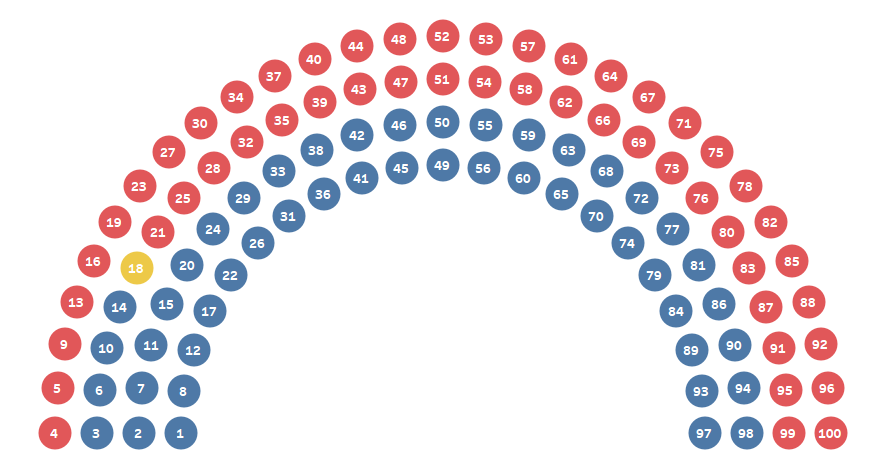
Ideally, I’d be able to then place each seat # (from the data) in the right location. To do that, I ended up performing a Cartesian join (or cross-join) of the data to itself. A Cartesian join essentially matches each record in one table with each record in another. So, this gave me each seat matched up with every other seat. I then wrote a calculated field to throw out the records that are not needed (those which don’t match the chart order shown above). This finally gave me the order I needed.

Unfortunately, this solution still had one flaw. In order to populate the chart in the right order, the data needed to be sorted and numbered sequentially according to that sort order (in the case above, the party). While it’s probably not unreasonable to ask people to perform such data prep prior to building one of these charts, I decided to take it one step further and make it the sortable by any dimension. For instance, if your data had gender in it, you might want to sort and color by gender instead of party. To do this, I created another INDEX calculation to determine the proper ordering of the data, then updated the calculation noted earlier which filters out the unneeded record.

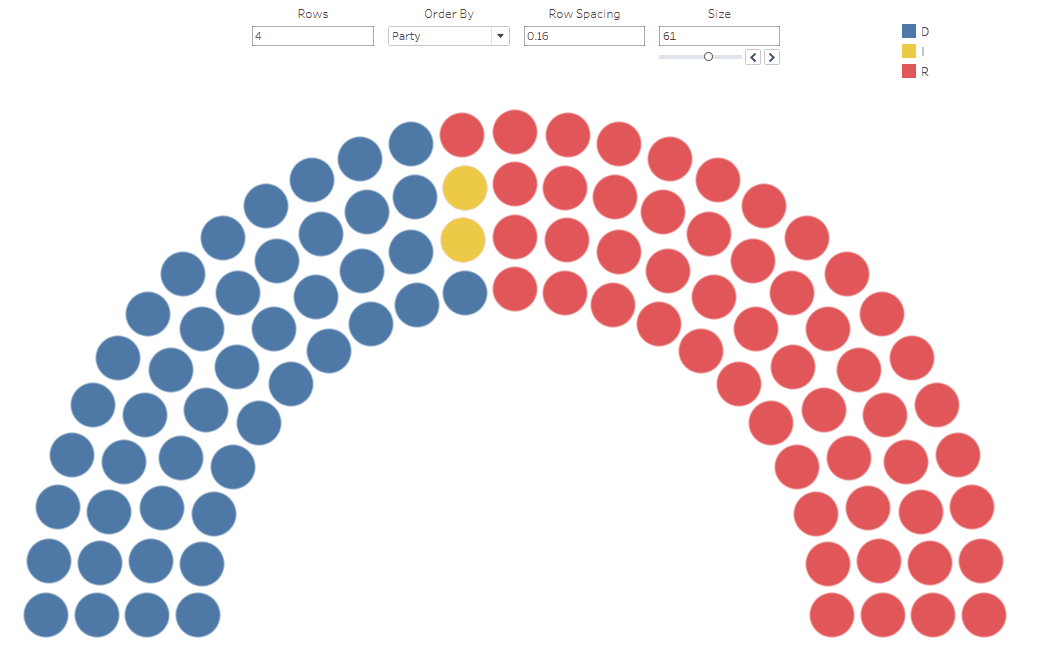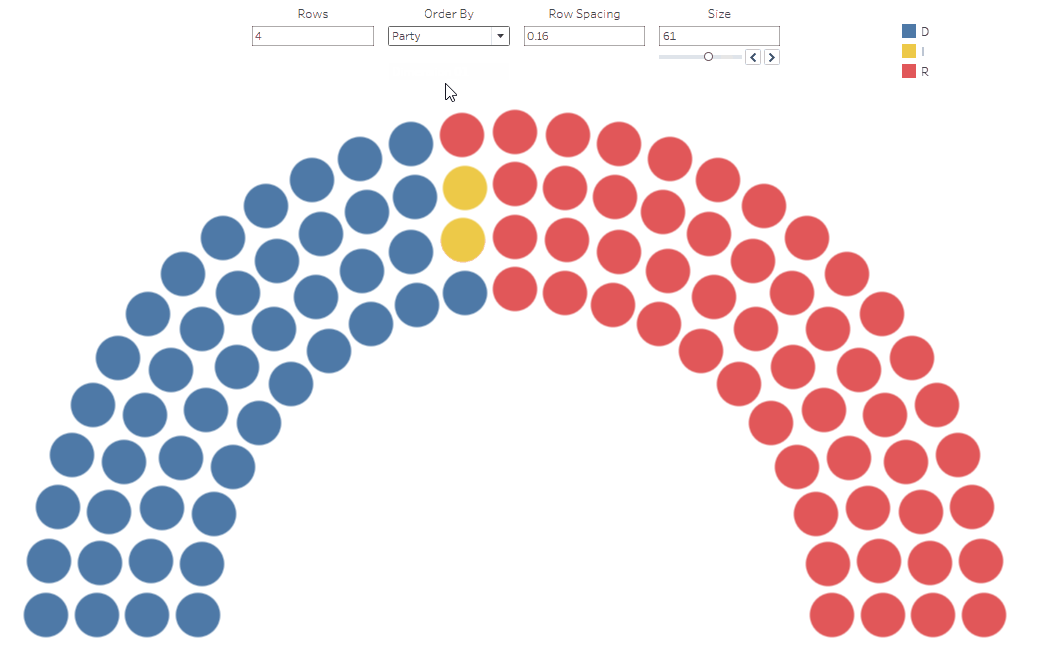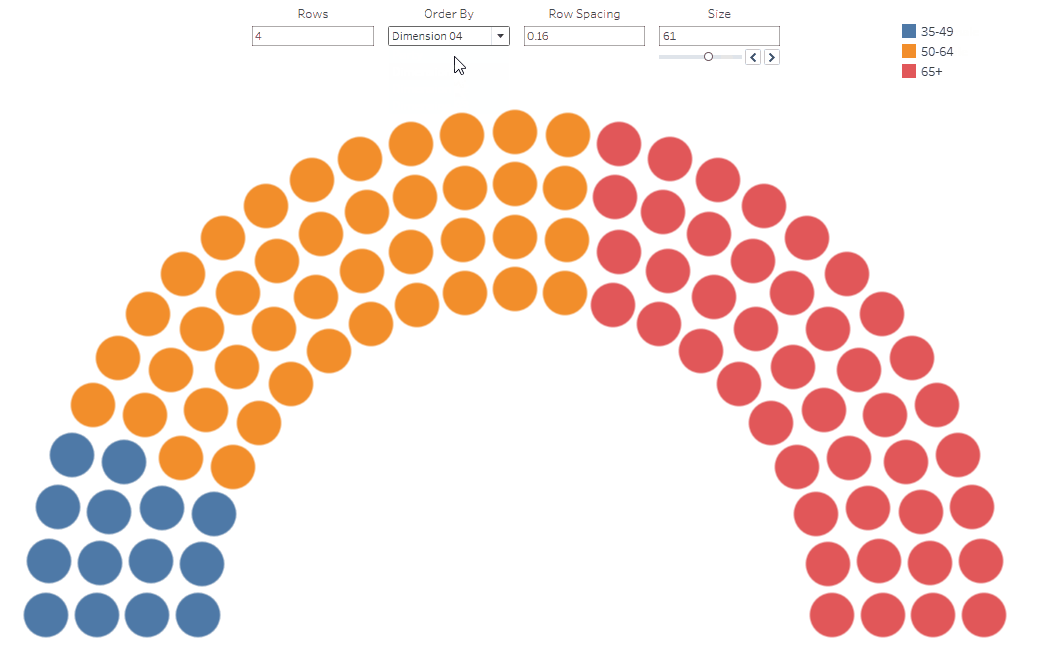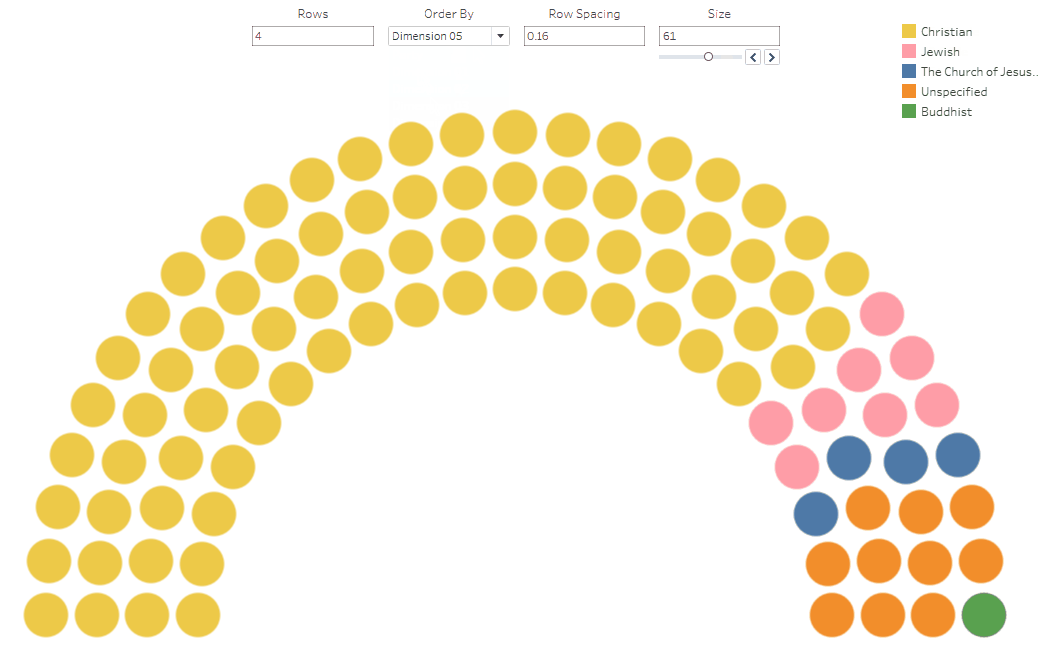
The Template

As promised, I’ve created a template for this chart. As with all of my templates, it includes an Excel workbook and a Tableau workbook. The Excel file looks like this:

Note: The template comes pre-populated with members of the 116^th US House of Representatives.

It contains the following fields:

Seat # – Unique identifier for the seat. No specific order is required—just make sure you have the ID and that it is sequential (don’t skip any numbers) and unique.

Party – Political party.

Member – Name of the member.

Dimensions 01-10 – These are user-defined dimensions you can use for whatever you like. My example above uses them for State, Gender, Race, Age, Religion, and Orientation. These are built into the sorting/coloring capabilities of the Tableau template, so be sure not to change the names in the Excel file (you can change them in Tableau, if you like).

Once you’ve populated all of your data, download the Tableau template, edit the data source and connect to your new data. In Tableau, you have a few different options for tuning the look and feel of your chart, using the following parameters:

Rows – Number of rows/arcs.

Inner Radius – Radius of the innermost arc. You can adjust this in order to push the inner arc outward or inward.

Row Spacing – Spacing between each row/arc. This is added to the inner radius to get the radius of each subsequent row/arc. Adjust this in conjunction with the inner radius in order to create the perfect spacing.

Size – Size of each dot. Ranged from 1 to 100.

Order By – Dimension on which you wish to order/color the chart. The parameter automatically includes Party and Dimensions 1-10. By default, the values will be sorted in ascending order. If you need to change the sort order, modify the sorting of the Order Field pill on the detail card.

Note: Dimensions 1-10 are all on the detail card in Tableau. This is to simplify the ordering/sorting if you choose to use one of these dimensions. It’s best to just leave all of them on detail to avoid the need to modify how the table calculations compute.

And that’s pretty much all you need to know. I will tell you that, due to the need for a Cartesian join—which significantly increases the number of records in the data set—and the table calculations—which add a lot of complexity—the performance isn’t always great. For smaller data sets, you won’t see many problems, but larger parliaments may take a few seconds to compute the calculations.

All the Files Can be Found Here

Alternatives

As you’ve seen, this was incredibly difficult to create. It’s certainly some of the most complex math I’ve applied to a chart. Additionally, as noted above, the need for a Cartesian join and multiple table calcs results in a chart that doesn’t perform quite as well as might be desired. But, perhaps more importantly, this simply may not be the best chart type for visualizing parliamentary makeup. The biggest problem with the chart is that its curvature makes it somewhat more difficult to read than other chart types (similarly to a pie chart). Thus, there are other alternatives that probably work better. And, as a bonus, they are much easier to create! So, let me provide a couple of those alternatives here.

In some case, you may just want to show aggregate totals, with no concern for individual members. In that case, a simple bar chart would be more than sufficient.

If the part-to-whole relationship is really important, then a stacked bar chart (or even a pie chart) might work.

I’d personally avoid this option for parliaments with more than 2 or 3 parties, unless your goal is to show some huge party juxtaposed with many other very small ones.

If you need to show individual members, then both of these charts can easily be converted into unit charts, allowing you to hover over each individual member for further details.

All this being said, I think there are times when a parliament chart might make a lot of sense. For one, it is something we generally recognize because of the shape—when I see one, I immediately assume that I’m looking at a country’s parliament. Ultimately, I think the problems with the chart are quite similar to the problems with pie charts, so following some of the same guidance is advisable. For instance, they can be effective when showing 2 or 3 parties (as with the US system), but there are much better alternatives for countries with more parties, such as Brazil, whose Chamber of Deputies currently has 25 different parties, resulting in a parliament chart, which is very difficult to read.

Wikipedia, By Parliament diagram tool, Public Domain

A bar chart is clearly a better alternative here.

I’d just advise you to think very carefully before using this chart type. As always, closely consider your data, your goal, and your audience first.

Ken Flerlage, January 27, 2020

Twitter | LinkedIn | GitHub | Tableau Public