Drawing Curves on a Map in Tableau (Guest Post)

I’m very excited to have Wendy Shijia join us today as a guest blogger. I’m sure you’ve seen Wendy’s work already. If not, what are you waiting for? Go check out her Tableau Public page right this minute! Wendy has created some absolutely amazing visualizations that combine her technical brilliance with fantastic analysis and storytelling, as well as phenomenal design.

Wendy is a Freelance User Experience Designer, based in Shanghai, China, and is very active in the Tableau community. You can find her on Twitter @ShijiaWendy and Tableau Public.

Background

In a recent viz, I visualized the data about the seeds at Svalbard Global Seed Vault. I was intrigued by their mission to protect the agricultural diversity for the whole world from future catastrophes. Since its opening in 2008, millions of seeds have been deposited by hundreds of countries. So I decided to build a viz around it and focus on the connections between the seeds and their source countries.

After some sketches, I came up with the idea of combining a map and a bar chart, linked with curves. 

  

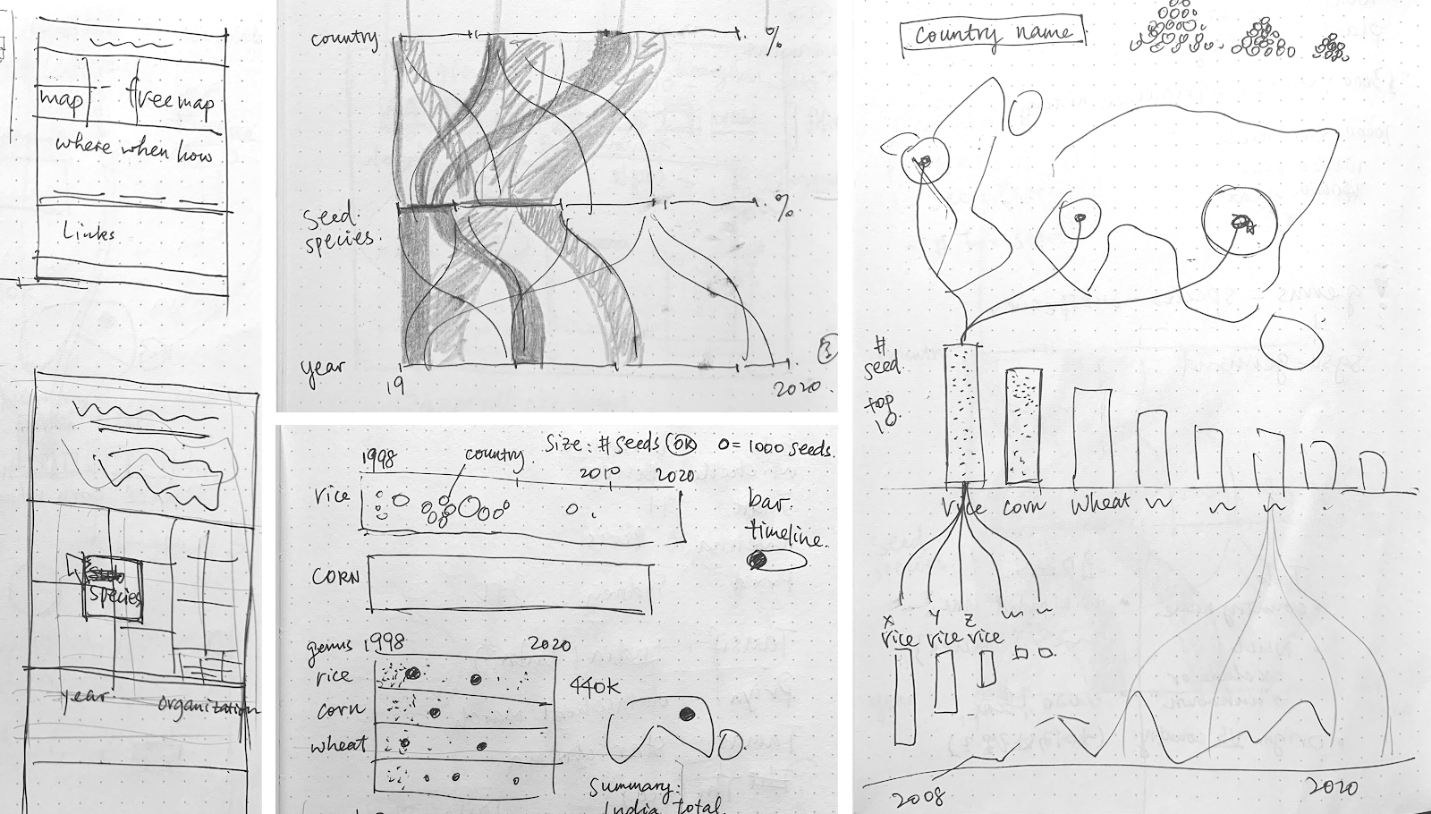
In thinking through the viz itself, I figured I could put the curves into a worksheet that would be layered on top of a map. However, it would be difficult to align Cartesian Coordinates (x, y coordinates) to a map that uses latitude and longitude. Let me explain. By default, maps in Tableau use the Mercator projection. In the Mercator projection, latitude and longitude lines are parallel, but there is some distortion caused by vertical lines being evenly distributed where horizontal lines are not.

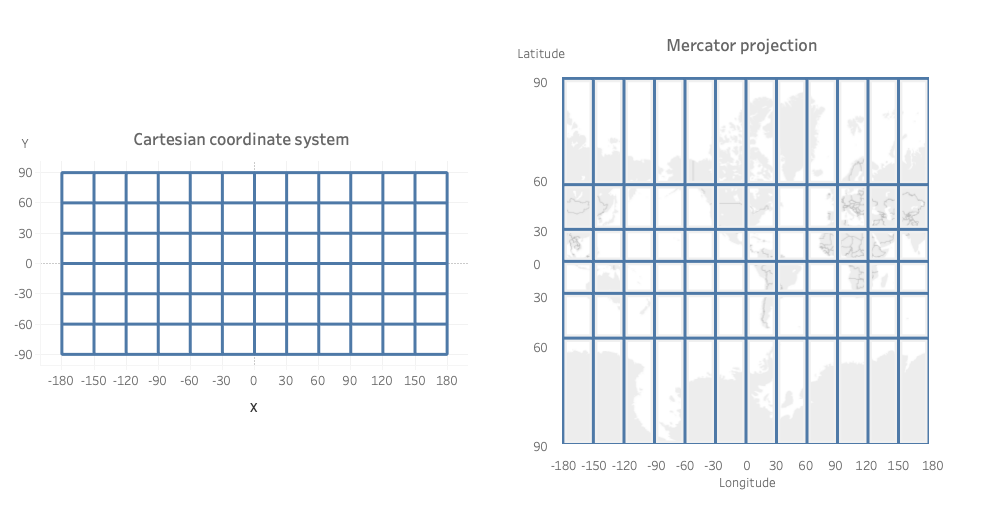
In Tableau, we typically draw curves using Cartesian coordinates (x and y), but you can see the issue this might cause when overlaying it on a map. So what if I drew the curves on the actual map instead? If I were to do this, the end of the curve would match exactly the location of a country, no matter how much the map distorts. So that’s what I decided to do.

Note: I’m going to be using sigmoid curves in this example, but this technique will work for other curve types as well. You’ll just need to change the formula used.

I found some techniques on the Tableau Magic website about drawing arcs on a map. I decided to employ a similar technique. As a quick intro, I started with a non-densified sigmoid curve, replaced x and y of each point with longitude and latitude, gave them geographical roles, and drew the curves on the map. I then overlaid a stacked bar chart in a separate worksheet at the bottom of the map. The curves aligned with the stacked bar chart, so it seemed like the source countries and seed groups were connected. 

If you’ve never created a curve before or simply need a refresher, please check out Ken’s blog post on Data Densification, which talks about drawing a sigmoid curve in detail. These techniques are foundational to the following tutorial, so if you are not familiar with them, please be sure to read Ken’s blog first.

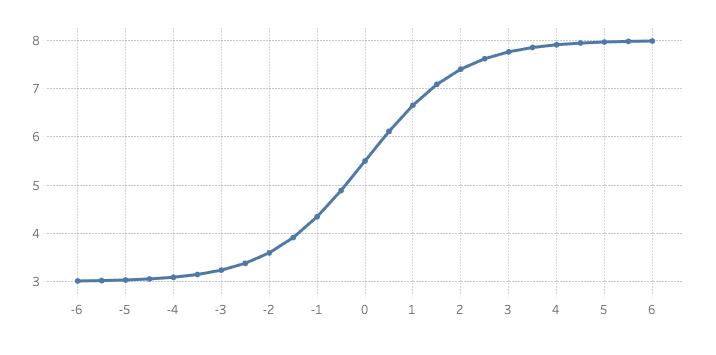
Before we start, let’s take a quick look at a sigmoid curve using standard X and Y coordinates. You’ll see that X is evenly distributed and the sigmoid function is applied to Y.

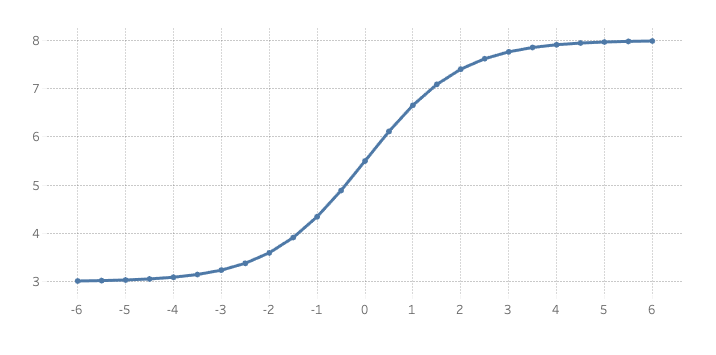
Now we will take this curve and turn it into a curve on a map. As mentioned, we will be converting Cartesian coordinates to geographical coordinates. I’m going to start with just one country and one grouping, so that we can demonstrate the technique. Then we’ll add in more countries and groups.

Okay, let’s go!

Step 1: Define Start and End Points

In my design, the curve starts from the bottom of the map (where the bar chart resides) and connects to the geographical location of each country. I started by simply defining the start point as calculated fields. We’ll tune these at a later stage.

startX: 0

startY: -90

Next, we need to create a data table with endX and endY (longitude and latitude) for each country (again, we’ll start with just one country). The fourth column “join” will be used to help generate points along the curve. (see step 3)

Step 2: Densify

As Ken detailed in his data densification blog, Tableau does not draw curves natively. Instead, we have to use densification to plot individual points, connected by lines. If we create enough of these line segments, the result is an approximation of a curve. To do this, we’re going to prepare a model table of 100 points. Why 100? This is just to ensure that we draw enough line segments to create a smooth curve.

The table has two columns, join and point. Like before, the join column will simply contain the word “link”. The point column will contain numbers 1 - 100.

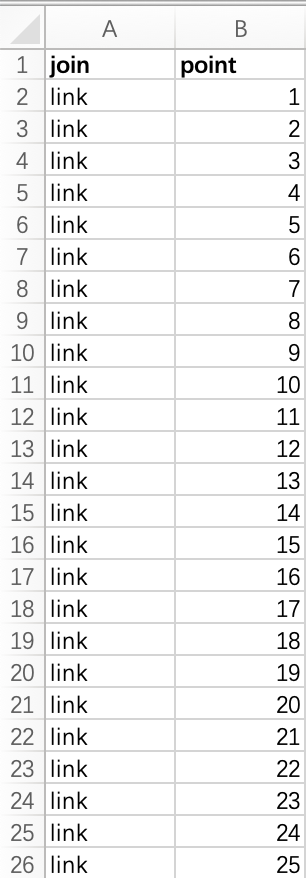
You’ll then join this data set to your original data set, joining on the join field.

This join will take our single row of data for our country and turn it into 100 rows of data. These 100 points will be used to draw the curve.

Step 3: Draw the Curves

To draw the curves, we need some calculated fields. The first just tells us the total number of points. We could use the data for this, but since we’re not planning to add more points, we can just hard-code it.

# point

100

Next, we’ll create a calculated field for the sigmoid function.

sigmoid

1/(1 + EXP(0.2)^ -(([Point]-([# point]+1)/2)*([endY-latitude]-[startY])/([# point]-1)))

You may adjust the number in red to change the smoothness.

Finally, we create calculated fields to get the X and Y coordinates for each point along the curve.

CurveX

[startX] + ([endX-longitude] - [startX]) * [sigmoid]

CurveY

[startY] + ([Point]-1) * ([endY-latitude] - [startY]) / ([# point]-1)

Now we’ll set the geographic role of CurveX to longitude and CurveY to latitude.

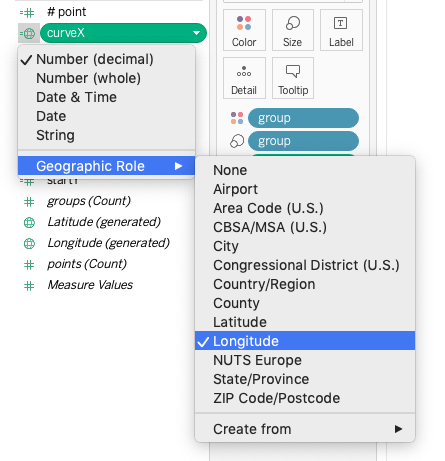
Next, drag CurveX to the columns shelf and CurveY to the rows shelf; change both to dimensions. Make sure the mark type is Line. If you’ve done it right, the sigmoid curve should now appear on the map.

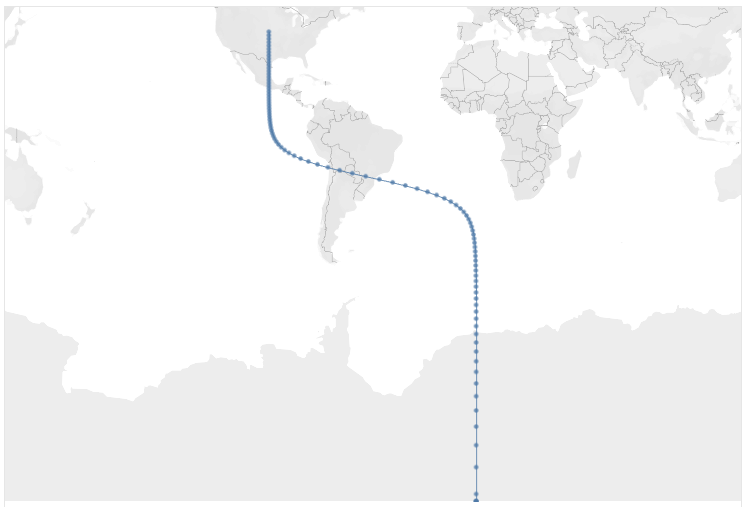
If you look closely at the above, you’ll notice that the curve is somewhat distorted. The curve is sort of pushed to the top, resulting in a long, straight line segment at the bottom. To help illustrate this, let’s look at the curve compared to a straight line and a sigmoid plotted using cartesian coordinates.

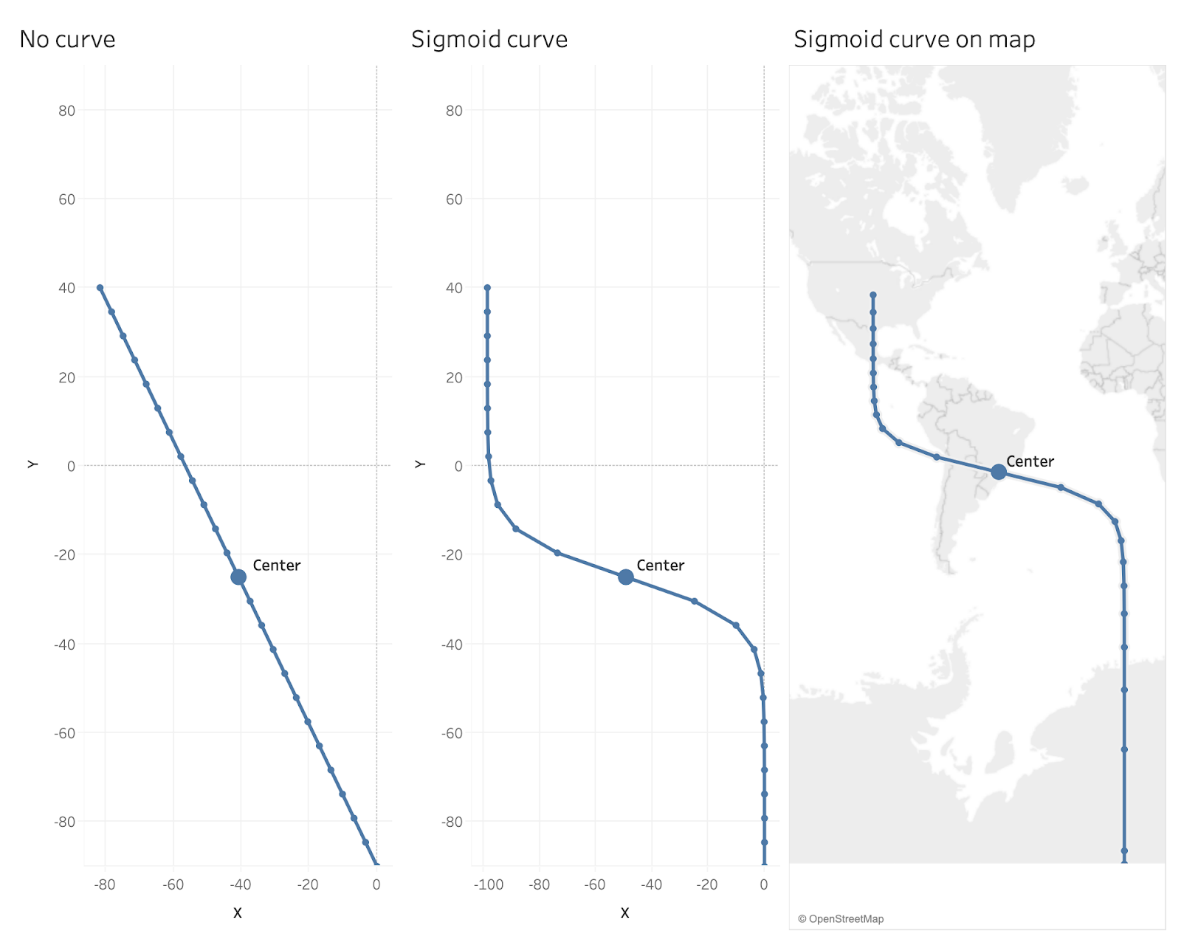
This is because of the distortion created by the Mercator projection, as noted earlier. This causes points at the bottom of the curve to be spaced further apart vertically, which makes the center point higher on the curve. That said, in our case, this is not of a lot of concern. I just want to make sure to point it out in case you notice it.

Step 4: Multiple Countries and Groups

Now we’ll add more countries into our original data set. We’ll also add in our different groups. Here’s an example using 3 countries, each with 3 groups.

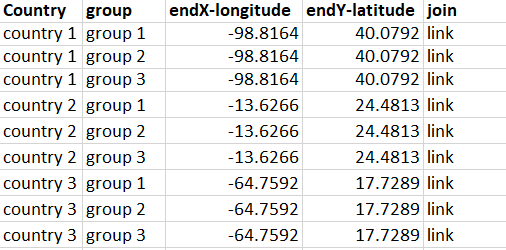
You’ll recall that we created a calculated field, startX for the horizontal position of the starting point. We set this to -90, but now that we have different groupings, we need them to start at different horizontal positions. So, we’ll edit the calculation to something like this:

startX

CASE [group]

WHEN "group 1" THEN -70

WHEN "group 2" THEN -50

WHEN "group 3" THEN -30

END

Now, when we plot the curves, we see separate curves for each country and each group, as shown below.

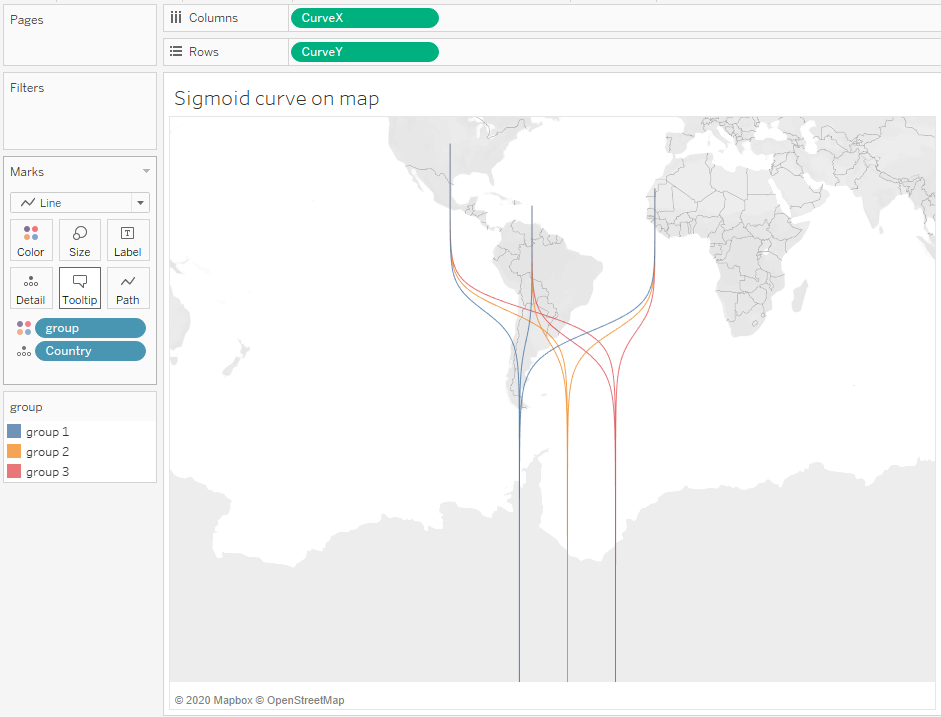
And that’s it! The data prep and calculations can be a bit tricky, but the result is quite lovely.

I want to reiterate something I mentioned earlier. While we’ve used sigmoid curves in this example, you could use any curve type you like. If you’re interested in learning about some other curve types, please check out the following blog by the brilliant Chris DeMartini: More Options for your Tableau Sankey Diagram

Thanks for reading. I hope this has been helpful. Have fun playing with your own data! And, if you have any questions, please feel free to contact me on twitter @ShijiaWendy

Wendy Shijia, August 17, 2020